A paper, “Infrageneric classification of Haworthia (Aloaceae): perspectives from nectar sugar analysis”, concerning the analysis of such sugars in Haworthia, Astroloba and Chortolirion was presented at the XV!th AETFAT Congress in Belgium in 2000, by G F Smith. B-E van Wyk, E M A Steyn and I Breuer. The proceedings of this Congress were published in Syst. Geogr. Pl. 71:391-397 (2001) and the particular paper by Smith et al was reprinted in Alsterworthia International 3(3)9-12 (2003). These authors comment on the taxonomic difficulties in trying to determine true generic limits in the tribe Alooideae of the Asphodelaceae and presented analyses of a limited number of taxa from the tribe. I, in turn, want to use that paper to show why the difficulty persists.
Smith et al cite my paper of 1972 where the main message was that the genera in this group would never be resolved while the main elements within the genus Haworthia were not recognized to be discrete. Uitewaal’s attempt to subdivide Haworthia was a much labored effort. He was clearly a victim of his time trying to establish a hierarchical classification and it is a distortion of the facts to say that he divided Haworthia into two main groups. There is no difficulty whatsoever in recognizing that he identified and recognized THREE, and not the two claimed by Smith et al. Uitewaal recognized two groups; Triangulares and Hexangulares based primarily on the shape of the flower base, and then he split Hexangulares into Robustipedunculatae and Gracilipedunculatae, primarily on the robustness of the peduncle. As an interested observer of Haworthia, I added the additional facts of geographic distribution and capsule and seed morphology to implement those three groupings as sub-genera.
I have always argued that the relationship of Haworthia and Astroloba would never be understood until it was recognized that the differences within Haworthia exceeded those between this genus and Astroloba.
It is significant, and this is the one great merit of the Smith et al paper, that the results show that Haworthia subgenus Haworthia does differ significantly from both the other two subgenera in respect of quite a fundamental property, viz. characteristics of the nectar sugars. Where the paper is weak is in respect of other detail. The problems are:-
- the question of whose classification was used
- the discussion in respect of sections within subg. Haworthia
- the provenance of the material used [this needs to be expanded on later].
- failure to provide a statistical parameter for the figures given.
With regard to 1 and 2, the authors seem to have used my classification in respect only of sub-genera and this is only evident in the way they order their derived data. In respect of the species they appear to have used their own expertise. I made it clear that there was no basis for the recognition of sections within the subg. Haworthia as presented by either Pilbeam or Breuer.
Provenance (3) is a problem for me because I know that identification without locality data is mostly not possible within that subgenus. It is thus imperative that a better vouchering of specimens is needed than this “trust me” approach. This is particularly true of the material cited for H. arachnoidea. Here it is important to know that the species is confounded with H. mucronata, and thus the listing also of H. habdomadis and H. unicolor. Similarly this is also true for the relationship of H. emelyae and H. comptoniana, or H. truncata and H. maughanii. Furthermore, there is no sense at all in listing H. mcmurtryi under “miscellaneous” taxa when surely any observer with some knowledge of the plants would know that it belongs in the Hexangulares with H. koelmaniorum.
With regards to 4, the failure to provide a statistical measure of variation of the sugar concentration levels is also a problem. Beyond the obvious group differences, there is no way in which any meaningful statement can be made about the figures for the subg. Haworthia. Where the authors do comment that the sugar ratios vary for plants taken from different localities, there is no guide as to how much these ratios may vary within, say, one population or even one individual plant. The comparisons they make for H. bolusii, H. cooperi and H. habdomadis var. morrisiae (6:39:55, 5:39:56 & 2:48:50), described as similar, and then for H. decipiens and H. semiviva (7:51:42 & 16:52:32) as different, in relation to some obscure classification into (sections ?) subsections or series, is simply confusing, and this is not only because I would disagree with that suggested relationship. I find it much more remarkable to see that the figures for H. arachnoidea (sample 2) is similar to H. unicolor (5:50:45 & 5:45:50), which is a probable truth if these two entities are considered as closely related, and to see that H. divergens and H. semiviva have exact similarity (both 16:52:32), which is a very probable untruth on geographical and morphological grounds. One could perhaps conclude that the sugars information demonstrates that there are no significant differences within the subg. Haworthia to support the author’s intitial contention, that there are. It is rather unlikely that, within a particular alooid group (e.g. subg. Haworthia), each species will have a unique nectar sugar profile. Rather it is more likely that similar (or dissimilar) profiles will have arisen many times, both between species, within species, or even within populations.
There is a further claim by the authors that they find “the correlation of nectar in Astroloba and members of the subg. Robustipedunculares with the sucrose-rich Hexangulares type”, surprising. For some quite undisclosed reason “floral and other morphological features” suggest to them that “these two units” (which two?) would be nearer to Aloe. In other words an element is introduced at the close of the paper suggesting a generic solution not broached in the preceding discussion. This could have been avoided had there been a properly ordered hypothesis that the exercise was set out to test. An answer to my question “which two?”, is irrelevant given the pointlessness of their statement. It is curious that Manning and Smith (Bothalia 30:53, 2000) dismiss hexose dominance in the nectar of Poellnitzia when they include that species in Astroloba
Listing the species, H. glauca, under the subg. Haworthia as Smith et al have done is an obvious typing error as the species belongs in the subg. Hexangulares. The usage of the phrase “obsolescently zygomorphic” to describe the flowers of Haworthia adds a quaint dimension to an old problem of definition of the term zygomorphic.
My conclusion, also based on the analysis of several other papers which have appeared in peer-reviewed technical journals, is that often the writers do not in fact know the subject, nor are they properly familiar with the literature.
Some very puzzling papers have been written in recent time that seem to dumb-down classification (of Haworthia, at least) to the levels of perception of the early 20th century. These include a paper on the cladistics of the alooideae, one on the cytology of Gasteria, another on the small Madagascan aloes, a paper on Poellnitzia, a paper on the DNA of the lesser genera of the Alooideae, and now this one on nectar sugars. These papers are all peripheral to the energies of six or more aspirant taxonomists who pontificate on the species and varieties of Haworthia, and the seemingly numberless hordes of enthusiasts who seemingly heedlessly, and often namelessly, express their views on the subject. Behind all this is my own effort to understand, and through written communication, comprehend what the elements are of Haworthia – what names are needed to effectively circumscribe the different “species” and to describe them.
My attempts to generate a key to species and some kind of hypothetical (evolutionary) tree simply failed. Intuitively, and I have to say intuitively because my intellectual and academic skills limit my capacity to do it better any other way, I recognized that we have been indoctrinated to think in terms of the logical rules of points, lines and symmetrical curves. I myself entered the fray by writing an article that discussed classification as art versus science, and have subsequently thought that perhaps I should have included politics as a third candidate. However, that discussion solved no problems and that of the classification of Haworthia still remains.
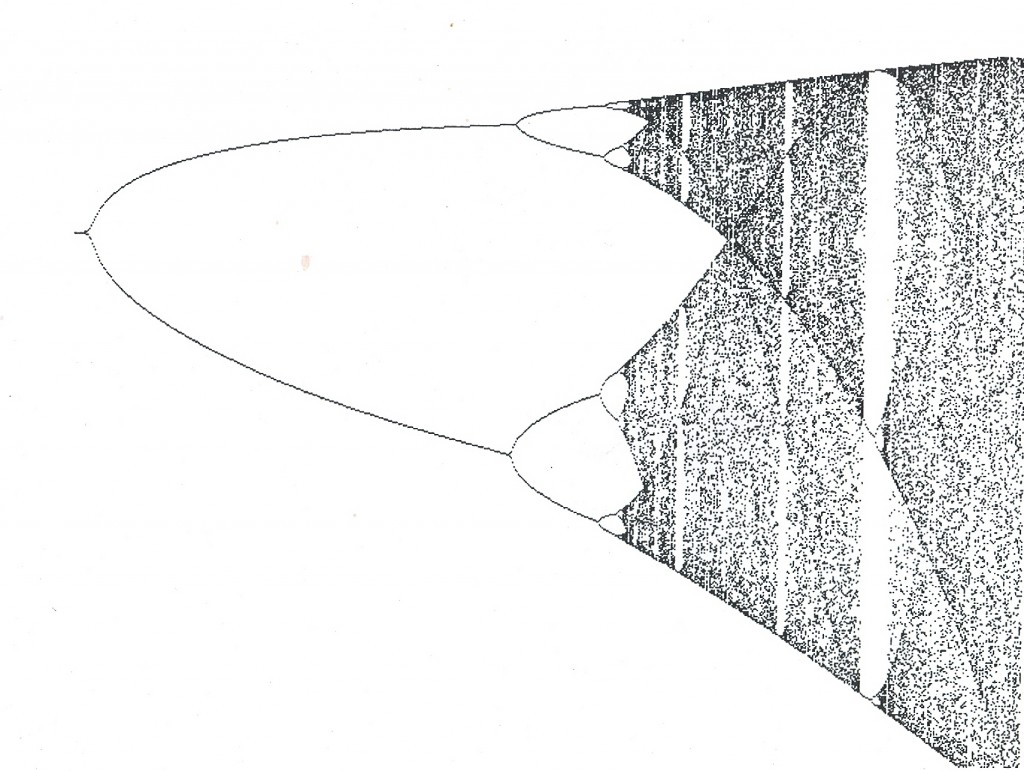
It was in reading a book by James Glieck entitled “Chaos, Making a new Science” that I felt I began to see the reason for our inability to agree on classification. In that book Glieck presented a diagram (see fig. 1) that he described as a bifurcation diagram and for which he did not give the algebraic function. The diagram appealed to me as a visual image of the problem of species and their recognition. In the book “Fractal Vision” by Dick Oliver, the same diagram appears together with the mathematical function that describes it. It is the non-linear function p2 = rp(1-p) and it was derived by an ecologist Robert May to describe population (p) growth with time (r)..
What the diagram suggests to me is that species and their individual variations can be described mathematically. It suggests to me that it is possible for species to be confounded by variation where the difference between two individuals or elements of one species is greater than the difference between two species.
Where I do have a problem is with the subject of cladistics. In my understanding this technique is simply an arithmetical way of dealing with many variables in such a way that it appears to be wholly objective. The problem for me is that it clearly is not because the character states and their evaluations remain subjective. Furthermore, it is entrenched in linearity giving truth to the quotation “the certainties of one age are the problems of the next”. Thus also my contention that botanists are at the trailing edge of science and largely lost in the Laplacean view that prediction and control of the universe was possible and simply a question of time while scientists unraveled a few remaining unknowns.
Coming back to figure 1, I need to say that I cannot state what the elements are of the function which depicts a classification tree (viz. cladogram, phylogenetic tree) instead of that of population growth. Perhaps g2 = rg(1-g) could be appropriate – where g is a group of “species” and r is (rate of) change. The value 1 would represent space and when fully occupied there would be only species? This raises an important issue and this is the significance of the planar or two-dimensional figure we use to illustrate relationships as a “tree”. Anyone would surely agree that species are phenomena distributed in space and that they change with time – an axiom. Therefore the planar model is inadequate as in effect it means that time is one axis and that space is also a single axis. It would be far more realistic to try to model species for what they are and thus introduce the third dimension as a minimum requirement. A secondary problem to that of the cladistic tree is that it is always drawn as a standing tree whereas mathematical convention is that the determining variable is plotted on the horizontal and not on the vertical axis. Is this simply because taxonomists have never made the true connection between their “trees” and space/time?
Putting that aside, it is obvious that the function only provides a conceptual shell. I once used the analogy of the denial by scientists of continental drift on the grounds that there was no explanation for it, when my contention is that it would have been more reasonable and fruitful to have to have rather sought the mechanism. The graph is what I see and I am sure that other taxonomists, of whatever academic stature and truly familiar with their plants, must see it too. Thus someone with the competence needs to search for the mathematical expression of the evolutionary and selection realities by which such a graph can be generated.
I contend that it could be useful to consider that the starting point of the graph need not be zero and neither that it moves forward in arithmetical progression. One can imagine that the undifferentiated cloud at point r = 4 as the starting point – the individuals of an ancestral widely distributed species. Imagine further the slowing down of change (r) and a breaking up of the distribution to restricted areas of space and the generation of isolated populations. Once so isolated there is the opportunity for “evolution” of population character and difference between populations. Speed up change again and expand the distribution area and the process is reversed. This is the equivalent of “pulsed” evolution remembering that a primary corollary of phylogeny is that it is irreversible. A particular point of interest is the change of pattern – that where one sees a systematic build-up from one to two, to four to eight; the system can collapse again to three or just one.
The point then to consider is now what function is truly appropriate for the modeling of a classification? Molecular biology and the use of DNA analysis is now in fashion. It is said that the difference between a mouse and an elephant amounts to 3% of their DNA – the difference between man and a chimpanzee even less. The sequence of the nucleotide bases on the chromosomal DNA is known to be indicative of similarity and it is used to identify even individuals. Therefore it is evident that if the DNA sequences were known that characterized any discrete group, the arrangement of the bases in that sequence, or set of sequences, would be what to look at to determine subgroups.
All very well – if we assume that there are subgroups and that they can be represented in a hierarchical classification.
Oliver quotes Christopher Alexander “We cannot produce order on the world-wide scale of everyday life without first having a clear picture of order itself, in the realm of ordinary objects. And this requires a completely new view of geometry…. Space must be considered an almost living entity… a kind of stuff which, according to the recursive structures that are built up in it, becomes progressively more and more alive”.
There is a paper by Verne Grant in American Journal of Botany 90:1263-1270 (2003) entitled “Incongruence between cladistic and taxonomic systems” which suggests that these are two rival schools in plant classification with different conceptual frameworks. The thrust of this paper of mine, and many others which I have authored, is that no two taxonomists seem to have the same concepts. Verne makes the unverifiable claim that “taxonomists… routinely study their plants in the field and garden, where feasible, as well as in the herbarium. These contacts build up a body of background knowledge and perceptions about the plants, which is hard to quantify but which contributes to sound taxonomic decisions”.
Grant’s paper is simply another which will never produce an answer. The perception is that a taxonomic opinion, however it is derived, must be expressed in the nomenclature of the group concerned. The sad truth is that taxonomists are not making sound decisions and if they are, these are not measurable except by the same subtleties that lead to good judgment. This is the fundamental weakness in classification. It is thus not empirical science but the generation of information which may require more intuitive wisdom and practical common sense than intellect to organize.
Acknowledgement:
This paper was written in two parts and various persons have commented on either or both. These are Messrs. Harry Mays, Paul Forster, Andrew Wilson and Steven Hammer. I am grateful for their input.
Footnote:
In considering the formula p2 = rp(1-p) which generates this diagram resembling a “species tree”, I think the variables can perhaps be identified as follows…
P = individual realised variation?
R = a space, time, genetic, morphological and behavioral value?
1 = the sum total of potential individual variation?
Perhaps it should also be noted that particle physicists speculate on the number of dimensions that are required to adequately explain creation.